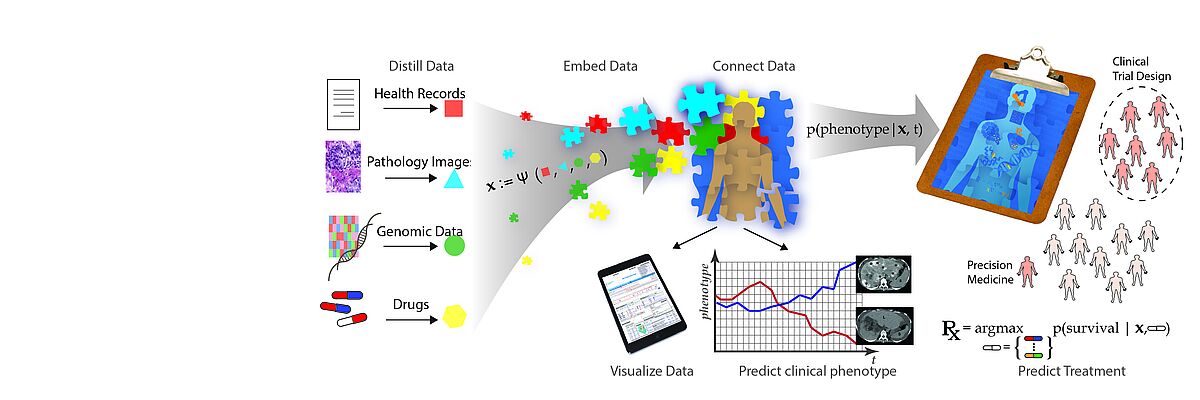
The BMI lab bridges research in Machine Learning and Sequence Analysis methodology research and its application to biomedical problems. We collaborate with biologists and clinicians to develop real-world solutions.
We work on research questions and foundational challenges in storing, analysing, and searching extensive heterogeneous and temporal data, especially in the biomedical domain. Our lab members address technical and non-technical research questions in collaboration with biologists and clinicians. At the research group’s core is an active knowledge exchange in both directions between the methods and the application-driven researchers.
The emergence of data-driven medicine leverages data and algorithms to shape how we diagnose and treat patients. Machine Learning approaches allow us to capitalise on the vast amount of data produced in clinical settings to generate novel biomedical insights and build more precise predictive models of disease outcomes and treatment efficacy.
We work towards this transformation mainly but not exclusively in two key areas. One key application area is the analysis of heterogeneous data of cancer patients. For Genomics, we develop algorithms for storing, compressing, and searching extensive genomics datasets. Another key area is the development of time series models of patient health states and early warning systems for intensive care units.
Publications
Abstract Fatigue is one of the most prevalent symptoms of chronic diseases, such as Multiple Sclero- sis, Alzheimer’s, and Parkinson’s. Recently researchers have explored unobtrusive and continuous ways of fatigue monitoring using mobile and wearable devices. However, data quality and limited labeled data availability in the wearable health domain pose significant challenges to progress in the field. In this work, we perform a systematic evaluation of self-supervised learning (SSL) tasks for fatigue recognition using wearable sensor data. To establish our benchmark, we use Homekit2020, which is a large-scale dataset collected using Fitbit devices in everyday life settings. Our results show that the majority of the SSL tasks outperform fully supervised baselines for fatigue recognition, even in limited labeled data scenarios. In particular, the domain fea- tures and multi-task learning achieve 0.7371 and 0.7323 AUROC, which are higher than the other SSL tasks and supervised learning baselines. In most of the pre-training tasks, the performance is higher when using at least one data augmentation that reflects the potentially low quality of wearable data (e.g., missing data). Our findings open up promising opportunities for continuous assessment of fatigue in real settings and can be used to guide the design and development of health monitoring systems.
Authors Tamás Visy, Rita Kuznetsova, Christian Holz, Shkurta Gashi
Submitted CHIL 2024 (PMLR)
Abstract Spatial transcriptomics enables in-depth molecular characterization of samples on a morphology and RNA level while preserving spatial location. Integrating the resulting multi-modal data is an unsolved problem, and developing new solutions in precision medicine depends on improved methodologies. Here, we introduce AESTETIK, a convolutional deep learning model that jointly integrates spatial, transcriptomics, and morphology information to learn accurate spot representations. AESTETIK yielded substantially improved cluster assignments on widely adopted technology platforms (e.g., 10x Genomics™, NanoString™) across multiple datasets. We achieved performance enhancement on structured tissues (e.g., brain) with a 21% increase in median ARI over previous state-of-the-art methods. Notably, AESTETIK also demonstrated superior performance on cancer tissues with heterogeneous cell populations, showing a two-fold increase in breast cancer, 79% in melanoma, and 21% in liver cancer. We expect that these advances will enable a multi-modal understanding of key biological processes.
Authors Kalin Nonchev, Sonali Andani, Joanna Ficek-Pascual, Marta Nowak, Bettina Sobottka, Tumor Profiler Consortium, Viktor Hendrik Koelzer, and Gunnar Rätsch
Submitted MedRxiv
Abstract This study advances Early Event Prediction (EEP) in healthcare through Dynamic Survival Analysis (DSA), offering a novel approach by integrating risk localization into alarm policies to enhance clinical event metrics. By adapting and evaluating DSA models against traditional EEP benchmarks, our research demonstrates their ability to match EEP models on a time-step level and significantly improve event-level metrics through a new alarm prioritization scheme (up to 11% AuPRC difference). This approach represents a significant step forward in predictive healthcare, providing a more nuanced and actionable framework for early event prediction and management.
Authors Hugo Yèche, Manuel Burger, Dinara Veshchezerova, Gunnar Rätsch
Submitted CHIL 2024
Abstract A prominent challenge of offline reinforcement learning (RL) is the issue of hidden confounding: unobserved variables may influence both the actions taken by the agent and the observed outcomes. Hidden confounding can compromise the validity of any causal conclusion drawn from data and presents a major obstacle to effective offline RL. In the present paper, we tackle the problem of hidden confounding in the nonidentifiable setting. We propose a definition of uncertainty due to hidden confounding bias, termed delphic uncertainty, which uses variation over world models compatible with the observations, and differentiate it from the well-known epistemic and aleatoric uncertainties. We derive a practical method for estimating the three types of uncertainties, and construct a pessimistic offline RL algorithm to account for them. Our method does not assume identifiability of the unobserved confounders, and attempts to reduce the amount of confounding bias. We demonstrate through extensive experiments and ablations the efficacy of our approach on a sepsis management benchmark, as well as on electronic health records. Our results suggest that nonidentifiable hidden confounding bias can be mitigated to improve offline RL solutions in practice.
Authors Alizée Pace, Hugo Yèche, Bernhard Schölkopf, Gunnar Ratsch, Guy Tennenholtz
Submitted ICLR 2024
Abstract In this paper, we explore the structure of the penultimate Gram matrix in deep neural networks, which contains the pairwise inner products of outputs corresponding to a batch of inputs. In several architectures it has been observed that this Gram matrix becomes degenerate with depth at initialization, which dramatically slows training. Normalization layers, such as batch or layer normalization, play a pivotal role in preventing the rank collapse issue. Despite promising advances, the existing theoretical results (i) do not extend to layer normalization, which is widely used in transformers, (ii) can not characterize the bias of normalization quantitatively at finite depth. To bridge this gap, we provide a proof that layer normalization, in conjunction with activation layers, biases the Gram matrix of a multilayer perceptron towards isometry at an exponential rate with depth at initialization. We quantify this rate using the Hermite expansion of the activation function, highlighting the importance of higher order (≥2) Hermite coefficients in the bias towards isometry.
Authors Amir Joudaki, Hadi Daneshmand, Francis Bach
Submitted NeurIPS 2023 (poster)
