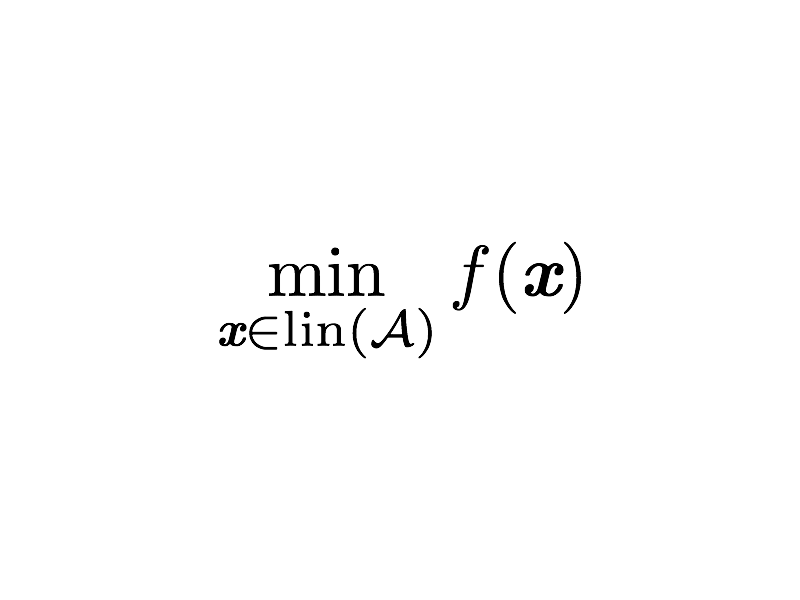Francesco Locatello*, Anant Raj*, Sai Praneeth Karimireddy, Gunnar Rätsch, Bernhard Schölkopf, Sebastian U. Stich, Martin Jaggi
Steepest Coordinate Descent is a special case of Matching Pursuit. This is particularly important as, while the CD rates can be deduced from the MP rates, the literature on CD is currently much richer than the one on MP. Understanding the connection of the two classes of CD and MP-type algorithms is a main goal of this paper, and results in benefits for both sides of the spectrum.
Two popular examples of first-order optimization methods over linear spaces are coordinate descent and matching pursuit algorithms, with their randomized variants. While the former targets the optimization by moving along coordinates, the latter considers a generalized notion of directions. Exploiting the connection between the two algorithms, we present a unified analysis of both, providing affine invariant sublinear $O(1/t)$ rates on smooth objectives and linear convergence on strongly convex objectives. As a byproduct of our affine invariant analysis of matching pursuit, our rates for steepest coordinate descent are the tightest known. Furthermore, we show the first accelerated convergence rate $O(1/t^2)$ for matching pursuit and steepest coordinate descent on convex objectives.
(Published at ICML and Presented at ISMP)
https://arxiv.org/pdf/1803.09539.pdf